Plug-and-Play ADMM on Image Super Resolution Problem
Project on testing performance of Image Super Resolution Problem using various denoisers as the variable of interest
TL;DR
- A class project in a graduate Machine Learning class
- Using MATLAB, we tackled the inverse problem of solving the image super resolution (SR) problem via plugging in different denoisers to see if the denoising performance causally affects the SR results, measured with PSNR.
- After testing with various state of the art denoisers, we found that a uniformly superior denoiser does not strictly imply a stronger candidate of a denoiser to be plugged into the ADMM algorithm, due to the contradiction of results of FFDNet being positively correlated and DnCNN being vague.
- Google Drive for all codes, figures, and data
- Paper
Given an observed degraded image, we would like to find the true image which is also being further corrupted with noise, assuming it is a additive white gaussian noise (AWGN). This task of recovering the true image is an inverse problem of image restoration, which in this case we are considering a subset of that, called Image Super Resolution (SR) problem. The problem aims to increase the resolution of an image which this can be understood as a maximum-a-posteriori (MAP) estimation problem. Then, we can use the scheme that make an unconstrained optimization problem to be reformulated as a constrained one which is a technique called Alternating Direction Method of Multiplier (ADMM).
The process of converting the unconstrained optimization problem into a constrained one splits the problem into subproblems which could be more optimally solved. With some assumptions such as likelihood and prior requirements of being closed, proper, and convex, so that they can guarantee convergence of the subproblems. Then, we can look at the star of the show, Plug-and-Play ADMM (PnP) framework, which is basically replacing one of the subproblems, specifically the part that deals with the prior of the model, with the off-the-shelf image denoisers. This stems from the fact that the update of an intermediate variable is trying to minimize the residue between the clean image and another temporary variable via the use of prior. From that, Venkatakrishnan et al. has proposed that this subproblem can be simplified further as just using the denoiser by injecting in the temporary variable to get the updated intermediate variable. Note that this framework has had many variations which each of them having their own pros and cons.
By modeling the image SR task with a forward model (likelihood) consisting of two operations: an anti-aliasing filter and a sub-sampling process, we can then attempt to solve this inverse problem by using PnP algorithm below:

Then, we used the MATLAB toolbox originally from Stanley Chan, who is the professor teaching the course, to run through the overall PnP framework. However, before getting to test different denoisers as a variable of interest on the SR performance, one could see the need of testing or validating the denoising performance of the denoisers in order to proceed, which we had done by adding the AWGN to the standard test images from the Set12 dataset, and apply various state of the art denoisers, in this case are Recursive Filter (RF), Non-local Means (NLM), Block-matching and 3D Filtering (BM3D), Total Variation (TV), Deep Convolutional Neural Network (DnCNN), and Fast and Flexible Denoising Convolutional Neural Network (FFDNet). The denoising performance is being measured via PSNR in dB with respect to different noise levels, shown below in Figure 2.
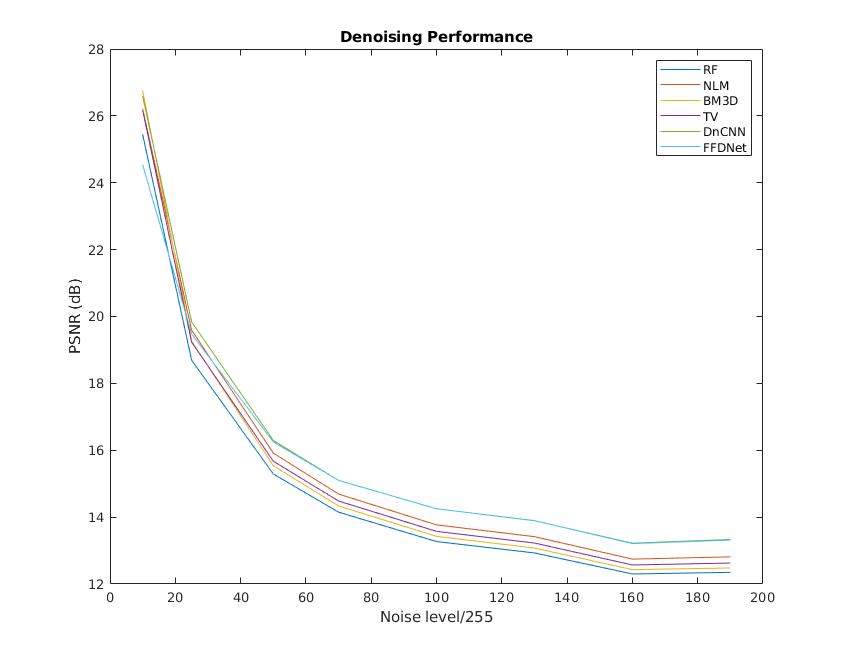
One can see that the DnCNN and FFDNet performs uniformly better than other denoisers, and based on our hypothesis, we posit that both of these denoisers would outputs better SR performance than that of other denoisers. However, one will see in Figure 3 and 4 below that the SR performance of noisy image has the same trajectory as that of the denoising performance alone in Figure 2, but the SR performance is not uniform, unlike the denoising task. Specifically, Figure 4 shows that the BM3D denoiser performs better at lower noise levels, but the FFDNet performs better at the higher noise levels, which brings us back to Figure 2 such that the relationship in denoising task seems to be the same, although the discrepancy in lower noise levels are almost indiscriminable. Note that the red trace depicts the monotone update of the hyperparameter configuration, blue trace depicts the original PnP scheme, and black curve depicts the adaptive update scheme which is precisely the algorithm shown in Figure 1.
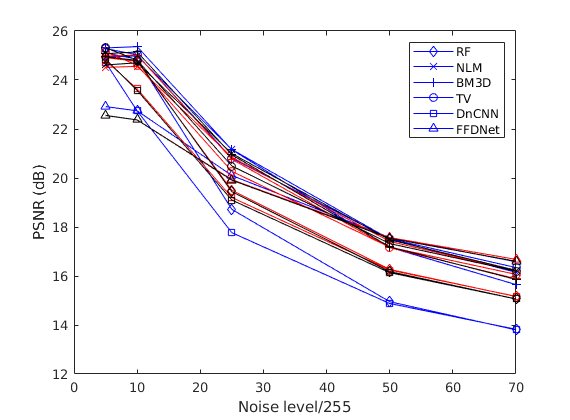
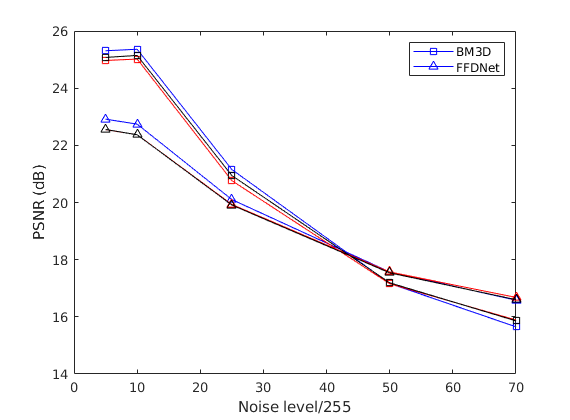
Conclusion and Possible Future Directions
From this, we have come to a conclusion that the uniformly superior denoiser does not strictly imply a stronger candidate of a denoiser to be plugged into the ADMM algorithm. However, one must note that there is a room for improvement in terms of amount of data being used, even though we have used a standard image dataset, the number of image being used in the quantitative experiment is considerably low, 10. Also, if the denoiser is in MATLAB code, one could try plugging in more advanced and recent state of the art denoisers to verify our results.